プロフィール:高齢子育て中、飲酒は週末のみ
特技:奥さんをフォローすること(嘘)
プロフィール:ゆとり世代(さとり世代)、独身、潔癖症
特技:インターネット超高速検索
【ルール】家庭でもカジノでも、人気のトランプゲーム「ブラックジャック(別名:21)」
ブラックジャック(英語: Blackjack)は、トランプを使用するゲームの一種。カジノで行われるカードゲームではポーカーやバカラと並ぶ人気ゲームである。カードの合計点数が21点を超えないように、プレイヤーがディーラーより高い点数を得ることを目指す。バカラやおいちょカブと似たスタイルのゲームである。
マジック、手品、バカラ、ブラックジャック、ポーカー、マジックカード、マジックトランプ様々なシーンで愛されるU.S.P.C社製のカードです。
ブラックジャックのルールも載っています。子どもと遊ぶのにもいいかも。
【感想】システムトレード界隈で時折話題になる、映画『ラスベガスをぶっつぶせ』(2008年)を観た

出典:、映画『ラスベガスをぶっつぶせ』(2008年)のチラシ裏面
『ラスベガスをぶっつぶせ』(原題: 21)は、2008年公開のアメリカ映画。原題の「21」はブラックジャックの別名。ラスベガスで実際に起きた、ブラックジャックのカードカウンティング事件を題材としたベン・メズリック(英語版)の小説『ラス・ヴェガスをブッつぶせ!』(Bringing Down the House, 2003年)の映画化。MITブラックジャック・チームが描かれており、このチームはマサチューセッツ工科大学などの学生や卒業生で構成され、ブラックジャックのカードカウンティングをするチームである。モデルとなったジェフ・マーも端役で出演している。
アメリカでは2008年3月28日に公開され、2週連続で興行収入1位を獲得。日本では同年5月31日に公開された。
驚異的な数学力を巧みに操り“カジノで数百万ドルを稼ぎだした”実話に基づく頭脳派サスペンス!
マサチューセッツ工科大学の学生ベン(ジム・スタージェス)は、天才的な数学力をローザ教授(ケヴィン・スペイシー)に見出され、ブラックジャックの必勝法(=カード・カウンティング)を習得するチームに誘われる。進学したい大学への30万ドルという高額な学費を稼ぐためベンは仲間とともにトレーニングを続け、卓越した頭脳と巧みなチームワークを駆使してラスベガス攻略に挑むが――!?
主人公のベン(ジム・スタージェス)は、進学に必要な30万ドルを稼ぐため、カジノ攻略のメンバーに加わる。

カジノ攻略の首謀者であるミッキー・ローザ教授(ケヴィン・スペイシー)は、ベンの数学的な才能に期待している。ケヴィン・スペイシーは映画の制作者でもあり、自ら出演している。

カジノで不正を見張る強面のコール(ローレンス・フィッシュバーン)。実はコールとローザ教授は過去に確執があった・・・。

攻略メンバー同士、ベンとジル(ケイト・ボスワース)はやがて恋仲になるが・・・。

アメリカでは2008年3月28日に公開され、2週連続で興行収入1位を獲得しました。
2003年刊。映画の原作となったノンフィクションです。実話ですよ、実話!
【解説1】カードカウンティングとは?
カジノも恐れるブラックジャック必勝法「カウンティング」とは?
「海外カジノでプレイヤーが確実に勝てるゲームはブラックジャック(以下BJ)以外にありません。仮に元手が200万円だったとしたら、日当10万円は稼げます」
そう語るのは、20年前からBJのプロとして年間5000万円以上稼いでいるK田氏。BJといえば、プレイヤーの2枚のカードとディーラーが開いている1枚のカードを見て、ヒット(もう1枚カードを引く)かスタンド(カードを引かない)を決める「ベーシックストラテジー」が有名だが、必勝法とはそれを指すのだろうか?
「ハウスルールにもよりますが、ベーシックストラテジー通りにプレイした場合の期待値はマイナス0.4%。仮にミニマムベット3000円で12時間(約1200ゲーム)プレイし続けた場合の期待収支は、3000円×1200ゲーム×0.4%で約1万5000円のマイナスになります。いい勝負ですが、必勝法というには少し弱い。私が駆使しているのはカードカウンティングという手法です」
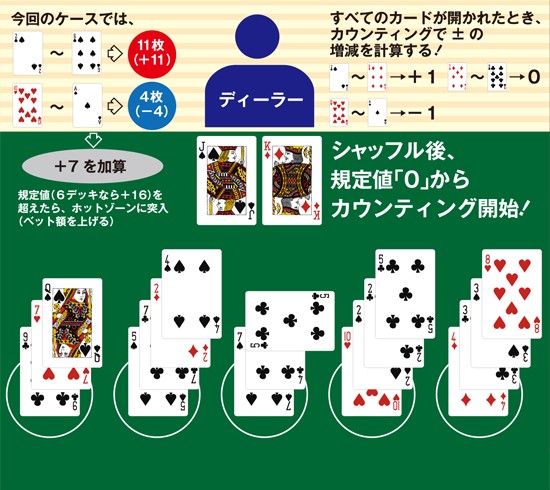
これは、1つのテーブルで使われるカードの総数が有限であることから、「すでに開けられたカードを記憶することで、残されたカードがプレイヤーにとって有利か不利かを見極めて、ベット額を増減する」という技術だ。
「残されたカードが10(絵札を含む)とAが多くなれば、プレイヤーにとって有利となります。逆に、2~6の低いカードが多ければ、ディーラーがバースト(22以上)する確率が減るので、プレイヤーにとって不利となる。ですから、シャッフル後、0からスタートして2~6のカードが開かれたら+1、10~Aのカードなら-1と増減を繰り返して、規定値(仮にカードを6デッキ使用していれば+16)に達したときにベット額を上げて利益を最大化します」
カウンティングを駆使したときの期待値はプラス1~2%。先の例でプレイ数を増やせば、日当10万円は稼げる計算になる。とはいえ、これだけ威力が高いとカジノ側にも対策されるんじゃ……。
「バレれば出禁です。ただ、カジノ側のカウンティング対策といわれるコンティニューシャッフリングマシン(ゲームごとにマシンがシャッフルしてカウントさせない)ですが、ある一定のプレイ数についてはシャッフルをしていないことが判明。期待値は1%程度に落ちますが、カウンティングが有効なことがわかりました」
でも、技術や才能は必要だな。若くて頭いい奴には中年の僕は勝てんだろ?
【解説2】変数変換とモンティ・ホール問題
モンティ・ホール問題
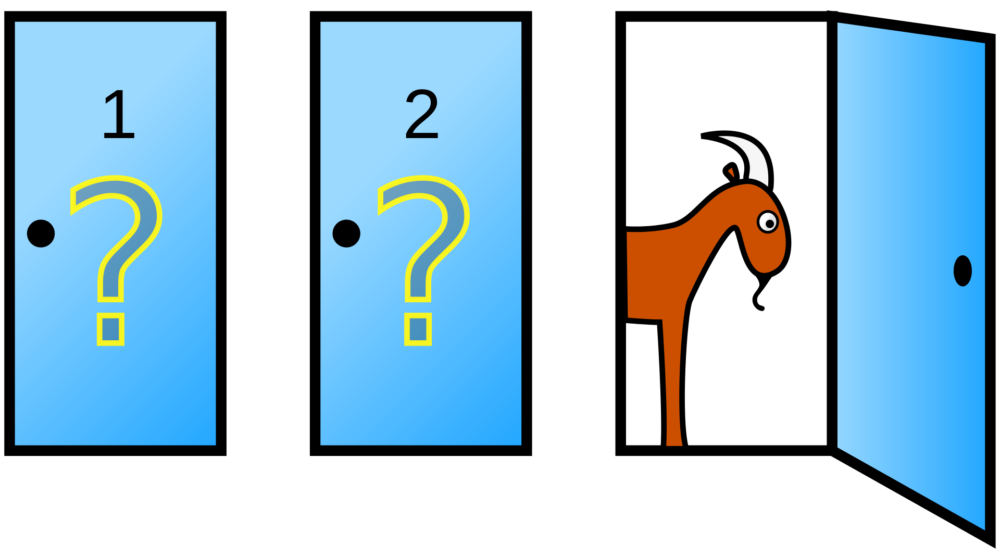
閉まった3つのドアのうち、当たりは1つ。例示のように1つのドアが外れとわかった場合、直感的には残り2枚の当たりの確率はそれぞれ1/2になるように思える。
モンティ・ホール問題
「プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。プレーヤーはドアを変更すべきだろうか?」
選択肢は2つ。ドアを変更する?
なんかひっかけみたいな気もするので、ドアは変更しません。
じゃあ、ちょっと説明を変えるね。
100枚のドアを使う方法
ゲームには100枚のドアが使われるとする。プレーヤーが最初のドアを選んだとき、このドアの当たりの確率は100分の1である。
モンティが残り99枚のドアのうち98枚を開けてヤギを見せる。
プレーヤーは2回目の選択をする。最初にプレーヤーが選んだ1枚のドアと「残り99枚のうちで、正解を知っているモンティが開こうとしなかった、ただ1枚のドア」の確率が相違していることは、直感で理解が可能であろう。
僕も最初はピンとこなかったけど、ドアの数を増やしてみると、直感的にしっくりくるようになった。
じゃあ、もうひとつ。「ためしてガッテン」の解説が意外にわかりやすかも。これならどう?
番組内で紹介したモンティ・ホール問題の説明
A、B、C、3つのドアがあり、ある人がAのドアを選んだ場合で考える。可能性は3つ。
車が「Aにある」、「Bにある」、「Cにある」。それぞれの確率は3分の1。順に考える。車がAにあった場合
司会者は、BかCのどちらかを開け、「選択を変えますか?」と聞く。どちらにしても、この時は、選択を変えるとハズレてしまうので、「変えない方が良い」。車がBにあった場合
このとき、司会者は必ずCのドアを開ける。なぜなら、Aは最初に選ばれたドアなので、開けられない(いきなり正解発表になってしまう)。Bは、車が入っているので開けられない(これも正解発表になってしまう)。Cが開き、車があるBが残る。選択はAからBに、「変えた方が良い」。車がCにあった場合
同様に、司会者が開けられるドアはBだけで、車があるCが残る。選択を「変えた方が良い」。3つの可能性のうち、2つで「変えた方が良い」ので、選択を変えた方が当たりやすい。
変数変換は、関数を使って元の数値を変換する方法です。
※Yahoo!知恵袋より
↓質問
変数変換とは何なのか、解り易く教えて下さい。↓ベストアンサー
例えばいま
Y={2(1+3X)-5}/(1+3X)^2
などという関数があったときに、
T=1+3Xとおくと
Y={2T-5}/T^2
と書き換えることができますよね?これはつまり、変数をXからTに変換しているということです(変数変換)
でも、さらにこっちの解説見るとわけわからなくなるから。
※Weblioは563の専門辞書や国語辞典、百科事典から一度に検索する辞書サイトです。
変数変換 transformation of variable
統計手法の多くは(1)母分布が正規分布であること,(2)各群の分散が等しい ことを仮定している。対数正規分布,二項分布,ポアソン分布などに従う変数はいずれの条件も満たさないので生のデータを使用して分析ができない。このような変数に数学的な変換をほどこし,新しく得られる変数が条件を満たすようにするための方法である。ただし,変数変換によって分析結果の解釈は必ずしも容易になるとは限らない。また,そもそも母分布について何の知見もないにもかかわらず,ある分布を仮定した変数変換を行うことはナンセンスである。逆に,理論的にある母分布が仮定できるなら,分析手法の要求する仮定にかかわらず変数変換を行わなければならない。いずれにせよ,変数変換を濫用してはならない。正規性,等分散性の仮定が満たされないような場合には,ノンパラメトリックな手法を検討したほうがよいであろう。
対数変換,角変換,平方根変換,プロビット変換,逆数変換,順序尺度化も参照のこと。
たぶん、ドアを変更するという行為が「変数変換」ってこと?
まあ、そんなとこだろ?
【妄想】いつか・・・「チキン・ディナー」(バカ勝ち)を!

「チキン・ディナー」(バカ勝ち)とはビニオンズ(Binion’s)の中国人ディーラーが言い始めた言葉。